Содержание
3. Некоторые практические соображения
4. Сравнение прироста информации
| Лефт.Ру |
Версия для печати |

|
Оригинал: http://www.wfu.edu/~cottrell/eea97.pdf
Перевод Юрия Жиловца
3. Некоторые практические соображения
4. Сравнение прироста информации
В этой работе мы хотим доказать, что трудовая теория стоимости является научной теорией в самом сильном смысле эмпирических наук. Вначале мы уточним, что мы считаем критериями научности, а затем покажем, что они практически выполняются для трудовой теории стоимости.
Научные теории говорят нам что-то о материальном мире. Это средства, с помощью которых мы одновременно объясняем и предвидим различные стороны реальности. Они не являются единственными средствами объяснения: мифы, сказки и религия также объясняют мир, но с более ограниченной способностью предсказания.
Теория, не делающая предсказаний, не может быть научной, а та, чьи предсказания не подтвердились, лишается права считаться наукой. Научная теория делает проверяемые предсказания. Обратите внимание, что под «предсказанием» мы не имеем в виду только предсказание будущего, хотя оно сюда тоже входит. Историческая наука может формулировать временные «послесказания» как логические предсказания. Научные предсказания дают информацию о мире, которая была недоступна в имевшихся ранее данных. Например, австралопитек жил задолго до Дарвина, но его существование – как «недостающего звена» - было выведено на основе теории эволюции гораздо позже. Такие предсказания предполагают применение какого-то общего закона к уже известным данным и получение производных данных, правильность которых может быть проверена. Производные данные не обязательно должны относиться к будущему или даже быть до того неизвестными, если только они не использовались в качестве входных.
Второй критерий – элегантность, выраженная в афоризме Уильяма Оккама «Сущности не следует умножать без необходимости». Если есть две теории, одинаково хорошо предсказывающие доступные данные, наука выбирает более простую. Система Птолемея плюс эпициклы могла бы победить теорию Ньютона, если бы последней не помогла простота.
Выбор простой теории отражает требования к предсказанию. Лучшее предсказание расширяет наше знание больше, пользуясь при этом меньшим количеством исходной информации. Теория с дополнительными эпициклами, специальными случаями и поддельными числами может хорошо предсказывать наблюдения... поскольку эти наблюдения лежат в самой ее основе.
Научный закон сжимает множество, даже потенциально бесконечное множество, наблюдений в простую формулу. Это машина для получения информации. В таком контексте мы снова вернемся к предсказаниям и простоте. Информация, полученная из закона, равна информации, полученной при применении закона, минус вложенная информация. Мы можем вложить информацию или в виде набора данных, к которому применяется закон, или в виде формулы, с помощью которой закон закодирован 1 . Хотя кодирование формулы должно, в принципе, включаться в любое измерение информационной стоимости теории, в рассматриваемой нами теории ценности мы будем считать длину всех формул примерно одинаковой, а длину входных данных - различной.
Будем рассматривать применение закона как применение функции , где
, где  означает закон,
означает закон,  - данные, к которым он применяется, а
- данные, к которым он применяется, а - полученные предсказания. Для правильного закона информационное содержание
- полученные предсказания. Для правильного закона информационное содержание должно превышать сумму информационного содержания
должно превышать сумму информационного содержания  и
и  . Первый критерий указывает, что предсказания не должны быть включены во входные данные; они должны быть новой информацией,
. Первый критерий указывает, что предсказания не должны быть включены во входные данные; они должны быть новой информацией,  не должно быть просто повторением
не должно быть просто повторением  . Теория может предсказывать входные данные, но она должна предсказывать еще что-то помимо них. Наш второй критерий, простота, гарантирует, что в сам закон не заложены заранее все его предсказания. Критерий прироста информации дает более строгую форму обоим критериям: сумма информации во входных данных и формулировке закона должна быть меньше, чем информация в полученных предсказаниях. Только тогда можно получить прирост информации (Solomonoff, 1964).
. Теория может предсказывать входные данные, но она должна предсказывать еще что-то помимо них. Наш второй критерий, простота, гарантирует, что в сам закон не заложены заранее все его предсказания. Критерий прироста информации дает более строгую форму обоим критериям: сумма информации во входных данных и формулировке закона должна быть меньше, чем информация в полученных предсказаниях. Только тогда можно получить прирост информации (Solomonoff, 1964).
Поведение случайных процессов не подчиняется какому-либо закону, и, следовательно, не может быть предсказано. Теория информации постулирует, что последовательность чисел случайна, если не существует формулы, более короткой, чем сама последовательность, способной ее породить. Неслучайная последовательность, напротив, имеет более короткий генератор. 1, 1, 2, 3, 5, 8 – вероятно, случайна, а 1, 1, 2, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 510, 887, 1397 – нет, поскольку вторую последовательность можно породить с помощью формулы Фибоначчи:

более короткой длины. Научный закон отражает неслучайное поведение реальности. Если мы рассматриваем как формулу закон и его входные данные, то эта формула должна быть короче, чем данные, которые получаются при его применении.
Цель нашей работы – использовать эти общие принципы для оценки относительных достоинств трех различных формул, предсказывающих наблюдаемые цены, а именно «стандартные» стоимости по Марксу (или вертикально интегрированные трудовые коэффициенты), цены продукции по Сраффе и цены продукции в интерпретации школы «Временнóй отдельной системы» (ВОС) (например, McGlone and Kliman, 1996). Мы знаем, что эти теории помимо предсказания реальных цен могут использоваться также для логических рассуждений, но мы будем считать их просто формулами, делающими предсказания.
В разделе рассматривается размер формулы, необходимой для построения трех вариантов предсказания цен.
Они получаются (в принципе, однако см. обсуждение практических сложностей в разделе 3) как вектор  длиной
длиной  , который решает уравнение
, который решает уравнение
 ,
,
где  есть матрица
есть матрица  технических коэффициентов, а
технических коэффициентов, а  - вектор длиной
- вектор длиной  непосредственных рабочих часов, затраченных на одну физическую единицу производства. Тогда требуемые данные -
непосредственных рабочих часов, затраченных на одну физическую единицу производства. Тогда требуемые данные -  технических коэффициентов и
технических коэффициентов и  коэффициентов непосредственного труда. Вектор решений обычно получается путем итераций
коэффициентов непосредственного труда. Вектор решений обычно получается путем итераций
 ,
,
которые завершаются, когда самый большой элемент вектора различий  становится меньше некоторой заданной точности.
становится меньше некоторой заданной точности.
Получаются как вектор  длиной
длиной  , который решает уравнение 2
, который решает уравнение 2
 ,
,
где скаляр  представляет общую норму прибыли, а
представляет общую норму прибыли, а  - вектор длиной
- вектор длиной  (прямых) зарплат, выплаченных на единицу произведенной продукции в каждой отрасли. Требования к данным здесь в сущности такие же, что и для вертикально интегрированных трудовых коэффициентов, но требуется дополнительная информация: норма прибыли (или реальная заработная плата, из которой можно получить норму прибыли). Расчет происходит примерно так же, например, с помощью итерации
(прямых) зарплат, выплаченных на единицу произведенной продукции в каждой отрасли. Требования к данным здесь в сущности такие же, что и для вертикально интегрированных трудовых коэффициентов, но требуется дополнительная информация: норма прибыли (или реальная заработная плата, из которой можно получить норму прибыли). Расчет происходит примерно так же, например, с помощью итерации

В ВОС цены получаются как сумма (заранее заданных) цен на входные компоненты плюс кратная доля совокупной прибыли. Обозначив такие цены через  , получаем:
, получаем:
 ,
,
где  обозначает заданный вектор входных цен в начале периода, остальные символы определены выше. Данных, требующихся для расчета этого вектора, определенно больше, чем для вертикально интегрированных трудовых коэффициентов и цен по Сраффе, поскольку кроме матрицы
обозначает заданный вектор входных цен в начале периода, остальные символы определены выше. Данных, требующихся для расчета этого вектора, определенно больше, чем для вертикально интегрированных трудовых коэффициентов и цен по Сраффе, поскольку кроме матрицы  и вектора заработной платы нам также требуется вектор цен на входные компоненты.
и вектора заработной платы нам также требуется вектор цен на входные компоненты.
Раздел 2 бегло упоминает некоторые затруднения, с которыми придется столкнуться при практическом использовании формул. В этом разделе обсуждаются две таких проблемы. Первая, с которой можно разобраться очень быстро, касается различия между основным и оборотным капиталом. «Учебное» представление расчета цен на продукцию (и в варианте Сраффы, и в варианте ВОС) предполагает чисто оборотную схему капитала. При этом не различаются основной капитал (по которому, предположительно, «должна» быть выравнена норма прибыли) и потоковое потребление капитала (измеряемое матрицей  таблицы входящих/исходящих потоков). Если отказаться от этого упрощения, становится ясным, что расчет цены продукции требует дополнительных данных – а именно, размера основного капитала по каждой отрасли – и вертикально интегрированные трудовые коэффициенты дают предсказания самым экономным образом.
таблицы входящих/исходящих потоков). Если отказаться от этого упрощения, становится ясным, что расчет цены продукции требует дополнительных данных – а именно, размера основного капитала по каждой отрасли – и вертикально интегрированные трудовые коэффициенты дают предсказания самым экономным образом.
Второй вопрос требует более полного обсуждения, поскольку касается самой сути проекта предсказания цен с помощью эмпирических трудовых стоимостей. В стандартном изложении принципа расчета стоимостей по Марксу начинают от данных по а) межсекторным потокам продукции в натуральных показателях и б) непосредственным рабочим часам, потраченным в каждом секторе экономики. Но статистика, доступная в капиталистических странах, не оставляет иного выбора, кроме использования данных, выраженных в денежных показателях. Вместо натуральных показателей, допустим количества угля, использованного в металлургии, или количества алюминия, использованного в самолетостроении, у нас есть только цифры денежной стоимости закупок каждой отрасли у других отраслей. Вместо вектора отработанных рабочих часов у нас есть вектор заработной платы.
Отсюда возникает проблема: если цены уже содержатся в данных, которые мы используем для расчета трудовых стоимостей, нет ли порочного круга в предсказании или объяснении цен на основе таких исходных данных? Реально это предположение ошибочно, но поскольку с первого взгляда оно кажется правдоподобным, мы рассмотрим его подробнее. Будет полезно различать два пункта: использование вектора зарплат как замены вектору отработанных часов и использование денежных межсекторных потоков (и результатов расчетов) вместо натуральных. Первый вопрос действительно представляет собой проблему (но, как мы считаем, не очень серьезную), а второй – нет.
Используя данные по заработной плате в качестве замены рабочим часам мы на деле рассчитываем вектор не самих вертикально интегрированных трудовых коэффициентов, а вертикально интегрированных коэффициентов издержек на заработную плату. Если бы зарплата была одинаковой во всех отраслях, это не играло бы никакой роли, но наличие разницы зарплат между отраслями все осложняет. Вопрос в следующем: какое отношение между разницей зарплат с одной стороны и различиями между секторами в «создающей стоимость» силе труда с другой стороны? Вот две противоположных возможности:
1. Разница в зарплате между секторами не имеет никакого отношения к разнице в создании стоимости: это неизбежный результат рынка или других социальных сил. В этом случае понятно, что «стоимости», рассчитанные с использованием заработной платы, будут очень неточной заменой «настоящих» стоимостей. Более того. Вероятно, что полученные таким образом цифры будут лучше коррелировать с рыночными ценами, чем с неизвестными «настоящими» стоимостями – поскольку издержки на зарплату по идее должны быть тесно связаны с действующей капиталистической практикой назначения цен – из-за чего сила предсказаний трудовой теории стоимости становится сильно преувеличенной.
2. Межсекторные различия в зарплате аккуратно отражают разницу в создании стоимости. Разница в зарплате отражает издержки на обучение, поскольку более обученные работники создают больше стоимости за час - или более точно, кроме действительного создания новой стоимости, переносят на продукцию трудовое содержание обучения. В этом случае показатели зарплаты в промышленности на деле являются лучшим приближением к теоретическим величинам, чем просто отработанные часы.
Как мы писали в другом месте, (напр. в Cockshott, Cottrell and Michaelson, 1995), истина определенно лежит где-то посередине между этими крайностями. Различия в зарплате между секторами частично отражают «настоящее» различие в производительности, а частично – внешние факторы. В любом случае, если структура затрат/выпуска экономики показывает достаточно сильную взаимозависимость, тогда вертикально интегрированные коэффициенты затрат на заработную плату для любого сектора будут содержать смесь труда из различных секторов, что более-менее устраняет влияние внешних факторов.
Необходимость работы с денежными стоимостями вместо натуральных показателей потоков является частично результатом степени агрегирования доступных таблиц затрат/выпуска капиталистических экономик. То есть, чтобы построить осмысленную таблицу затрат/выпуска в натуральных показателях, необходимо, чтобы данные были четко разделены по отдельным видам продукции. Однако многие отрасли, показанные в реальных таблицах, производят широкий набор различной продукции. Нельзя получить осмысленные показатели количества выпуска «Летательных аппаратов и их частей», или «Электрических компонентов и принадлежностей», или поток в натуральных показателях из второй отрасли в первую. Практическим решением будет представлять агрегированные денежные стоимости таких потоков.
Но это не создает проблему, если мы хотим сравнить совокупную денежную стоимость выпуска отраслей с совокупной трудовой стоимостью этого же самого выпуска. Идея в следующем: Вектор совокупных трудовых стоимостей сектора, рассчитанный из таблицы денежных стоимостей, будет согласован с вектором, рассчитанным по таблице натуральных показателей, с точностью до скаляра, независимо от вектора цен и (общей) доли зарплаты, использованных при построении таблицы денежных показателей. Или, иными словами, полученный вектор трудовых стоимостей сектора не зависит от использованного вектора цен. Можно было бы с тем же успехом (если бы это было практически возможным) для построения «денежной» таблицы использовать произвольный вектор цен или весов. Реально действующие цены, использованные в опубликованных данных, никаким образом не «заражают» полученные показатели; не вызывают появление фальшивых соответствий между стоимостями и ценами.
Доказательство
Рассмотрим экономику, характеризующуюся следующими массивами:
 - матрица
- матрица  натуральных потоков между секторами, так что
натуральных потоков между секторами, так что  представляет собой объем выпуска отрасли
представляет собой объем выпуска отрасли  , использующегося в производстве отрасли
, использующегося в производстве отрасли  .
.
 - вектор
- вектор  валового выпуска отраслей, в натуральных показателях.
валового выпуска отраслей, в натуральных показателях.
 - вектор
- вектор  непосредственных рабочих часов, отработанных в каждой отрасли.
непосредственных рабочих часов, отработанных в каждой отрасли.
Будет полезно определить также диагональную матрицу 
 , такую, что
, такую, что

Стандартный расчет трудовых стоимостей происходит следующим образом. Вначале рассчитывается матрица  технических коэффициентов как
технических коэффициентов как  и вектор длиной
и вектор длиной  непосредственного труда на единицу физического выпуска
непосредственного труда на единицу физического выпуска  . Тогда вектор длиной
. Тогда вектор длиной  стоимостей единицы продукции (вертикально интегрированных трудовых коэффициентов) равен
стоимостей единицы продукции (вертикально интегрированных трудовых коэффициентов) равен
 ,
,
а вектор длиной  совокупных стоимостей выпуска сектора равен
совокупных стоимостей выпуска сектора равен
 (1)
(1)
Теперь мы построим денежный аналог этих массивов. Пусть вектор  длиной
длиной  представляет цены товаров, а скаляр
представляет цены товаров, а скаляр  - (общую) ставку заработной платы 3 . Определим также диагональную матрицу
- (общую) ставку заработной платы 3 . Определим также диагональную матрицу 
 , такую, что
, такую, что
 .
.
Для каждого «настоящего» массива, определенного выше, имеется его денежная версия:
 - матрица денежных стоимостей потоков между секторами.
- матрица денежных стоимостей потоков между секторами.
 - вектор денежных стоимостей валового выпуска.
- вектор денежных стоимостей валового выпуска.
 - вектор зарплат в промышленности.
- вектор зарплат в промышленности.
С их помощью мы можем построить аналоги полученных «настоящих» массивов. Диагональная матрица 
 , диагональные элементы которой равны
, диагональные элементы которой равны  определяется как
определяется как
 (2)
(2)
Аналог матрицы технических коэффициентов равен
 (3)
(3)
Элементы  представляют стоимость в долларах продукции сектора
представляют стоимость в долларах продукции сектора  , необходимой для выпуска продукции в секторе
, необходимой для выпуска продукции в секторе  . И наконец, аналог
. И наконец, аналог  есть вектор длиной
есть вектор длиной 

 (4)
(4)
элементы которого представляет прямые затраты труда на каждый доллар выпуска продукции в каждом секторе.
Теперь возникает вопрос: предположим, что мы не владеем информацией о потоках продукции в натуральных показателях и рабочих часах, а имеем в своем распоряжении только информацию, данную в денежных таблицах. На их основе мы рассчитываем вектор  ,
,

Если  представляет собой вертикально интегрированные отработанные часы для каждой физической единицы товара
представляет собой вертикально интегрированные отработанные часы для каждой физической единицы товара  , то
, то  , которые мы можем получить из денежных таблиц, есть вертикально интегрированные затраты на труд на каждый доллар выпуска товара
, которые мы можем получить из денежных таблиц, есть вертикально интегрированные затраты на труд на каждый доллар выпуска товара  . Если мы умножим его на денежную стоимость валового выпуска всех отраслей, то получим вектор вертикально интегрированных затрат на труд для всех отраслей:
. Если мы умножим его на денежную стоимость валового выпуска всех отраслей, то получим вектор вертикально интегрированных затрат на труд для всех отраслей:
 (5)
(5)
Мы хотим знать зависимость между (1), совокупными стоимостями по секторам, которые в принципе можно получить из данных, выраженных в натуральных показателях, и (5), соответствующими показателями, полученными с использованием денежных данных.
На основе связи между (2), (3) и (4) мы можем переписать (5) как
 (6)
(6)
Вспомните, что в (1) указано  . Сравнивая эти два уравнения, мы видим, что
. Сравнивая эти два уравнения, мы видим, что  , при условии, что
, при условии, что
 (7)
(7)
То, что это условие действительно выполняется, видно, если взять обратные величины от обоих частей формулы (7); слева мы просто получаем  ; справа -
; справа -

Это означает, что мы доказали, что  , то есть что совокупные стоимости по секторам, полученные из денежных данных, согласуются – с точностью до скаляра
, то есть что совокупные стоимости по секторам, полученные из денежных данных, согласуются – с точностью до скаляра  - общей ставки заработной платы, с теми, что были бы получены из данных в натуральных показателях при их доступности. Вектор совокупной стоимости не зависит от вектора цен, использовавшегося при составлении денежных таблиц.
- общей ставки заработной платы, с теми, что были бы получены из данных в натуральных показателях при их доступности. Вектор совокупной стоимости не зависит от вектора цен, использовавшегося при составлении денежных таблиц.
Теперь мы можем вернуться к нашей главной теме, оценке трех версий теории стоимости в терминах предсказывающей мощности или прироста информации. Как мы показали, у трудовой теории стоимости самая простая формула, цены продукции по Сраффе немного сложнее, а цены продукции по теории ВОС имеют самую сложную формулу (если считать только входные данные). Более сложная формула может быть оправдана, если прирост предсказанной информации превышает дополнительную сложность формулировки.
Общее уравнение содержания информации или энтропии в последовательности символов выглядит следующим образом:
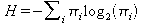 ,
,
где  - энтропия последовательности битов,
- энтропия последовательности битов,  - вероятность нахождения i-того символа, вероятности складываются по всей последовательности символов 4 . Определим наши символы как отношение
- вероятность нахождения i-того символа, вероятности складываются по всей последовательности символов 4 . Определим наши символы как отношение  , где
, где  - это рыночная цена, а
- это рыночная цена, а  - оценка рыночной цены или с помощью трудовой стоимости, или с помощью какой-то формы цены продукции. Определив наши символы таким образом, мы получаем условную энтропию вектора рыночных цен
- оценка рыночной цены или с помощью трудовой стоимости, или с помощью какой-то формы цены продукции. Определив наши символы таким образом, мы получаем условную энтропию вектора рыночных цен  при данном векторе оценок
при данном векторе оценок  . То есть
. То есть
 ,
,
где  , вероятность, что случайно выбранная единица продукции имеет отношение
, вероятность, что случайно выбранная единица продукции имеет отношение  , попадающее в
, попадающее в  малый интервал (ширина этих интервалов определяется точностью измерений).
малый интервал (ширина этих интервалов определяется точностью измерений).
В общем случае лучшей оценкой будет та, которая дает наименьшую условную энтропию вектора рыночных цен, поскольку это означает, что бóльшая часть информации в этом векторе уже закодирована в самой формуле оценки. Исходя из общего содержания информации в векторе рыночных цен  , мы можем рассчитать взаимную информацию или «трансинформацию» (Reza, 1961) как
, мы можем рассчитать взаимную информацию или «трансинформацию» (Reza, 1961) как  . Эта величина есть показатель уменьшения неопределенности относительно
. Эта величина есть показатель уменьшения неопределенности относительно  , достигаемая при предсказании
, достигаемая при предсказании  ; при прочих равных условиях мы хотим увеличить ее до максимума, но необходимо также принимать во внимание требуемое количество входной информации. В этом свете предельная предсказательная эффективность теории будет равна
; при прочих равных условиях мы хотим увеличить ее до максимума, но необходимо также принимать во внимание требуемое количество входной информации. В этом свете предельная предсказательная эффективность теории будет равна
 ,
,
отношению прироста трансинформации к приросту поступления информации для относительно более простой теории. Эта предельная предсказательная эффективность дает меру элегантности теории.
Чтобы провести эти расчеты, нам потребуются: 1) показатели общего содержания информации в векторе рыночных цен и 2) распределение вероятности для отношения  . Мы оцениваем содержание информации в векторе рыночных цен, предполагая определенную точность входных данных, а именно: показатели даны с точностью до 3 цифр или 9,96 битов точности. Тогда информационное содержание вектора рыночных цен будет равно: 47 отраслей по 9,96 битов в каждой, или около 470 битов. Точное количество цифр после запятой относительно неважно, поскольку более высокое
. Мы оцениваем содержание информации в векторе рыночных цен, предполагая определенную точность входных данных, а именно: показатели даны с точностью до 3 цифр или 9,96 битов точности. Тогда информационное содержание вектора рыночных цен будет равно: 47 отраслей по 9,96 битов в каждой, или около 470 битов. Точное количество цифр после запятой относительно неважно, поскольку более высокое  даст преимущество (то есть равным образом поднимет значение
даст преимущество (то есть равным образом поднимет значение 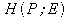 ) всем методам оценки.
) всем методам оценки.
Наши данные взяты из американской таблицы затрат/результатов 1987 года и показателей Бюро экономического анализа по основному капиталу за тот же год 5 . Данные бюро по сравнению с таблицей более агрегированы по заводам и оборудованию. Следовательно, мы должны объединить некоторые строки и колонки таблицы, чтобы гарантировать, что у каждой отрасли есть отдельная цифра, которой сопоставлены данные по заводам и оборудованию. В получившейся таблице 47 колонок и 61 строка. Колонки – создающие вместе с первыми 47 строками квадратную подматрицу, - представляют агрегированные группы отраслей. Остальные строки содержат:
Два последних пункта создают некоторые аналитические проблемы. На агрегатном уровне они, вероятно, являются частью прибавочного продукта, но с точки зрения фирм, которые уплачивают непрямые налоги и ренту, они представляются расходами. Пока существует тенденция к выравниванию нормы прибыли, мы считаем чистую прибыль, а не прибыль после уплаты непрямых налогов и рентных платежей. В отсутствие более удовлетворительного решения в настоящем исследовании мы просто исключили их из всех наших расчетов (т.е. удалили их из расчета и издержек, и прибыли).
Цифры БЭА даны по постоянному капиталу; мы предполагаем, что дополнительно отрасли располагают запасами переменного капитала, равным месячной себестоимости (причем себестоимость для расчетов по ВОС включает в себя зарплаты, а для расчетов цен по Сраффе – нет).
Необходимо отметить, что моделирование постоянного капитала – это логический двойник моделирования времени оборота. Мы предполагаем, что для совокупного капитала оборот переменного капитала составляет один месяц. Это предположение основано на сильных упрощениях: предполагается, что год состоит из 12 производственных периодов, соответствующих выплате месячной зарплаты, а общие запасы товаров в процессе производства и в цепях оптовой и розничной торговли равны продажам за месяц. То есть мы предполагаем, что время оборота переменного капитала - один месяц, и зарплаты выдаются авансом, а оборотный постоянный капитал закупается одновременно с рабочей силой. (При расчете цен по Сраффе мы предполагаем, что зарплаты выплачиваются в конце месяца). Более сложное исследование должно было бы изучить движение счетов фирм в каждом секторе экономики и построить модель реального работающего капитала. В отраслях, где производство основано на системах оперативной поставки, складские запасы гораздо меньше, следовательно, оборот – быстрее; для других отраслей оценка запасов в один месяц, наоборот, недостаточна.
Для расчета показателя общего выпуска по каждой отрасли при использовании трудовой стоимости и моделей по Сраффе использовались итеративные процедуры, описанные выше. Оценки ВОС общего выпуска получены одним проходом без преобразования исходных данных. Таким образом получены три оценки вектора совокупных цен; корреляции между этими оценками и наблюдаемыми ценами показаны в табл. 1.
Таблица 1. Корреляции между ценами по секторам экономики и их предсказанными значениями для 47 секторов американской промышленности
Наблюдаемая цена |
|
Трудовые стоимости |
0,983 |
Цены ВОС |
0,989 |
Цены по Сраффе |
0,983 |
Как вы видите, все оценки хорошо коррелируют с рыночными ценами, причем оценки по ВОС немного точнее остальных. Корреляции не взвешены; каждый сектор просто считался одним наблюдением. Мы также рассчитали корреляции между регистрациями переменных – в согласии с аргументом Шайха (1984) о накапливающейся ошибке в связи цена-стоимость. Распределение корреляции осталось неизменным (трудовые стоимости – 0,980, цены ВОС – 0,986, цены по Сраффе – 0,980). Мы также рассчитали взвешенные корреляции, веса назначались по предсказываемой переменной (то есть в случае трудовых стоимостей как доля общественного труда, затраченного в каждом секторе): в этом случае цены ВОС по-прежнему были точнее всех – корреляция 0,989, а трудовые стоимости (0,987) оказались впереди цен по Сраффе (0,985).
Для каждой отрасли мы затем рассчитали отношение рыночной цены выпущенной продукции к каждой из оценок, получив вектор отношений рыночная цена/стоимость, рыночная цена/цена ВОС и рыночная цена/цена по Сраффе. Энтропия этих векторов рассчитывалась следующим образом:
 была проинтегрирована в диапазоне от 0 до 3 с разбиением на 1000 шагов интегрирования. 1000 шагов дают максимально возможную величину интеграла равную
была проинтегрирована в диапазоне от 0 до 3 с разбиением на 1000 шагов интегрирования. 1000 шагов дают максимально возможную величину интеграла равную  = 9,96, то есть предполагаемой точности данных в таблицах. Интервал [0; 3] был выбран для интегрирования, поскольку плотность вероятности для всех оценок за пределами этого диапазона падает до нуля.
= 9,96, то есть предполагаемой точности данных в таблицах. Интервал [0; 3] был выбран для интегрирования, поскольку плотность вероятности для всех оценок за пределами этого диапазона падает до нуля.Получившаяся условная энтропия рыночных цен относительно каждой оценки показана в табл. 2. Четвертая строка в таблице показывает общее количество информации о ценах для 47 отраслей, которое может дать каждая из моделей. В терминах выхода информации модель ВОС превосходит модель Сраффа, а та превосходит модель трудовой теории стоимости.
В терминах исходной информации модели выстраиваются в прямо противоположном порядке, поскольку модель Сраффы требует дополнительного вектора из 47 элементов с данными о постоянном капитале, а модели ВОС нужен еще и вектор входных цен из 47 элементов. Сколько дополнительной информации содержится в каждом из этих векторов? Если мы предположим, что они точны до трех знаков, тогда в каждом из векторов содержится 468 битов. Но, вероятно, не имеет смысла требовать, чтобы данные о ценах и постоянном капитале были даны с такой точностью. Поскольку мотивацией для построения модели ВОС было как минимум воспроизвести марксистскую технику преобразования стоимостей в цены продукции, мы предположим, что данные по постоянному капиталу должны иметь точность не большую, чем цены, рассчитанные только по трудовым стоимостям – примерно 1,9 битов на показатель или 90 битов на весь вектор. Эффективность использования этой дополнительной информации в теории Сраффы довольно низкая: для каждого бита, добавленного к входным данным, к выходным данным добавляется примерно 0,15 бита.
Таблица 2. Расчеты энтропии (P – наблюдаемая цена, E1 – трудовые стоимости, E2 – цены ВОС, E3- цены по Сраффе.
(P|E1) |
(P|E2) |
(P|E3) |
|
Условная энтропия |
8,028 |
7,538 |
7,734 |
Потенциальная энтропия |
9,966 |
9,966 |
9,966 |
Трансинформация I(P4;E) |
|||
- для одного предсказания |
1,938 |
2,428 |
2,232 |
- для всех 47 отраслей |
91,09 |
114,12 |
104,90 |
За вычетом того, что уже известно о ценах |
0 |
-468 |
0 |
Чистое предсказание |
91,09 |
-354 |
104,90 |
Дополнительная входная информация |
0 |
90 |
90 |
Прирост информации на бит дополнительной входной информации |
- |
-3,93 |
0,153 |
Необходимо заметить, что требуемая дополнительная информация в обоих случаях сильно различается. В случае ВОС требующаяся дополнительная информация относится к переменной, которую модель и предсказывает, а именно к цене. В идеале мы должны предоставить для расчетов цены, запаздывающие всего на один период производства. При использовании таблиц затрат/результатов это невозможно, поэтому на деле мы используем текущие относительные рыночные цены. Учитывая, что данные по ценам в таблицах отражают средние цены за год – срок, значительно больший, чем любая правдоподобная оценка «периода производства» - разница между текущим и предшествующим периодом размывается. Использованные показатели относились к периоду с января по декабрь 1987 года. Предполагая разрыв в месяц между переменным и оборотным капиталом, идеально будет, если данные относятся к периоду с декабря 1986 года по ноябрь 1987 г. Поскольку два этих периода большей частью пересекаются, использованные показатели действительных цен должны быть очень хорошим приближением к тем, которые надо предсказать. Принимая это во внимание, оказывается, что предсказательная сила ВОС отрицательна. Мы получаем по ней оценку вектора цен менее точную, чем та, с которой начинали. Прирост информации (на деле – потеря) равна  бита. Предсказание с использованием непреобразованных входных цен дает чистый прирост информации только, если корреляция между вектором цен с 1.12.86 по 30.11.87 и между вектором 1.1.87-31.12.87 меньше, чем корреляция между оценкой по ВОС и вторым вектором.
бита. Предсказание с использованием непреобразованных входных цен дает чистый прирост информации только, если корреляция между вектором цен с 1.12.86 по 30.11.87 и между вектором 1.1.87-31.12.87 меньше, чем корреляция между оценкой по ВОС и вторым вектором.
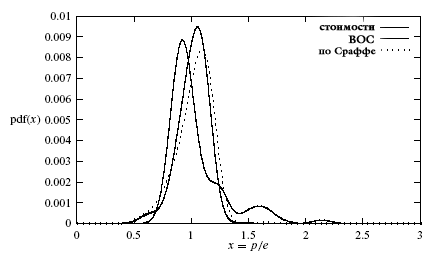
|
| Рис. 1. Функции плотности вероятности для наблюдаемого отношения цены к ее оценке. |
Большинство изложений теории стоимости наводят на мысль, что цены продукции по Сраффе должны предсказывать реальные цены намного лучше, чем простая трудовая теория стоимости (ТТС) 6 . Мы обнаружили, что это не так. Теория Сраффы работает примерно также, как ТТС, если мерять по корреляции и чуть-чуть лучше, если мерять по энтропии 7 . Этот факт требует объяснения. Понятно, почему предсказания по Сраффе не намного опережают ТТС – нормы прибыли вопреки Сраффе ниже в отраслях с высоким естественным накоплением капитала.
Это видно из табл. 3 и на рис. 2. В таблице показан коэффициент корреляции между нормой прибыли и накоплением капитала, а также между нормой прибыли и величиной, обратной накоплению, по всем 47 секторам. Первый коэффициент – 0,454 – статистически значим на уровне в 1%. Но если цены соответствуют простой ТТС, то мы должны обнаружить положительную линейную зависимость между нормой прибыли и величиной, обратной естественному накоплению (другими словами, связь между нормой прибыли и естественным накоплением должна быть обратной, а не отрицательной линейной), поэтому второй коэффициент, наверное, более показателен: при 0,780 он имеет значение p - предельный уровень значимости - меньшее 0,0001.
Таблица 3. Нормы прибыли и естественное накопление, постоянный капитал по БЭА плюс месячный оборотный постоянный капитал как оценка постоянного капитала (C). В каждом случае общая статистика взвешена по делителю.
s/C |
c/v |
s/v |
|
Среднее |
0,292 |
1,948 |
0,569 |
Стандартное отклонение |
0,221 |
3,042 |
0,500 |
Коэффициент вариации |
0,756 |
1,562 |
0,878 |
s/C и c/v (взвешенные по C) |
s/C и v/c (взвешенные по C) |
||
Коэффициент корреляции |
-0,454 |
0,780 |
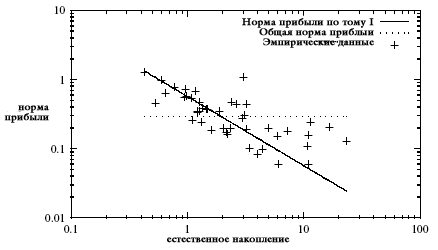
На рис. 2 показаны три набора точек:
|
| Рис. 2. Связь между нормой прибыли и естественным накоплением, постоянный капитал по данным БЭА плюс месячный оборотный капитал как оценка общего капитала (логарифмические шкалы) |
Отсюда видно, что наблюдаемая норма прибыли близка к нормам, предсказываемым теорией из первого тома «Капитала». Исключением являются несколько отраслей с необыкновенно высоким естественным накоплением > 10.
Но что это за отрасли? Похоже, что они относятся к двум категориям, и каждая действительно «исключительна». Во-первых, это регулируемые коммунальные услуги – электроснабжение и газоснабжение. Электроснабжение имеет естественное накопление в 23,15, а ее норма прибыли находится посередине между предсказанием простой трудовой теории стоимости и предсказанием по теории цены продукции. У газоснабжения норма прибыли в 20% при естественном накоплении в 10,4; трудовая теория стоимости предсказывает норму прибыли в 7%, а теория производства – 32%. В обоих случаях отрасль регулируется и конечно же система регуляции строится на предположении, что услуги должны давать среднюю норму прибыли. Во-вторых, имеются отрасли с высоким естественным накоплением, в которых главную роль играет рента. При накоплении в 16,4 продажа неочищенной нефти и природного газа имеет норму прибыли намного выше предсказываемой трудовой теорией стоимости и приближающейся к предсказываемой по выравниванию уровней прибыли. Но отрасль такого рода и должна, согласно теории дифференциальной ренты Рикардо, продавать свою продукцию выше средней стоимости, а, следовательно, и сообщать о более высокой прибыли. В том же положении находится нефтеперерабатывающая промышленность с естественным накоплением в 9,4. У добычи и переработки нефти похожая норма прибыли – 31% и 32%. Поскольку отрасль вертикально интегрирована, это показывает, что нефтяные монополии решили сообщать о своих сверхприбылях как заработанных пропорционально капиталу, вложенному в производство первого и второго передела. Но в обоих случаях прибыль можно объяснить с помощью дифференциальной ренты.
Как упоминалось выше, мы сейчас не располагаем независимыми данными о времени оборота в различных секторах, поэтому наши цифры по основному капиталу не полностью удовлетворительны. Самое большее, что мы можем сделать в этой работе, - это исследовать чувствительность результатов при изменении (общего для всех) предположения о времени оборота. Табл. 4 воспроизводит табл. 3 с учетом альтернативного предположения, что основной капитал в отрасли составлен из постоянного капитала по данным БЭА плюс зарплата на два месяца плюс оборотный постоянный капитал на три месяца. Корреляции, показывающие отрицательную или обратную связь между нормой прибыли и естественным накоплением, по-прежнему остаются статистически значимыми, и, как очевидно, не зависят от указанных изменений.
Таблица 4. Нормы прибыли и естественное накопление, постоянный капитал по БЭА плюс трехмесячный оборотный постоянный капитал и двухмесячная зарплата как оценка постоянного капитала (C).
s/C |
c/v |
|
Среднее |
0,239 |
2,218 |
Стандартное отклонение |
0,133 |
3,146 |
Коэффициент вариации |
0,558 |
1,418 |
s/C и c/v (взвешенные по C) |
s/C и v/c (взвешенные по C) |
|
Коэффициент корреляции |
-0,457 |
0,650 |
1 В строгом виде формула и входные данные должны быть выражены в форме, пригодной для интерпретации универсальной машиной Тьюринга. Хорошее изложение концепции машины Тьюринга можно найти в Penrose (1989).
2
Если считать, что зарплата выплачивается заранее, то указанное уравнение должно быть переписано в виде 
3 Разобрав выше проблему разницы зарплат между отраслями, мы теперь оставляем ее в стороне.
4 Обсуждение информации и энтропии см., например, в Reza (1961), Chaitin (1987).
5 Конкретно, данные по капиталу взяты из файлов wealth14-wealth17 на дискете 4 выпуска Бюро экономического анализа по Постоянному воспроизводимому материальному богатству в США, 1925-1989 гг.
6 За исключением Farjoun and Machover (1983).
7 Корреляция, зависящая от квадратичных ошибок, делает больший акцент на нескольких больших ошибках, а энтропия, зависящая от ошибок регистрации, подчеркивает большое количество малых ошибок – поэтому возможна разница при оценке по разным критериям.
| При использовании этого материала ссылка на Лефт.ру обязательна |
|
|